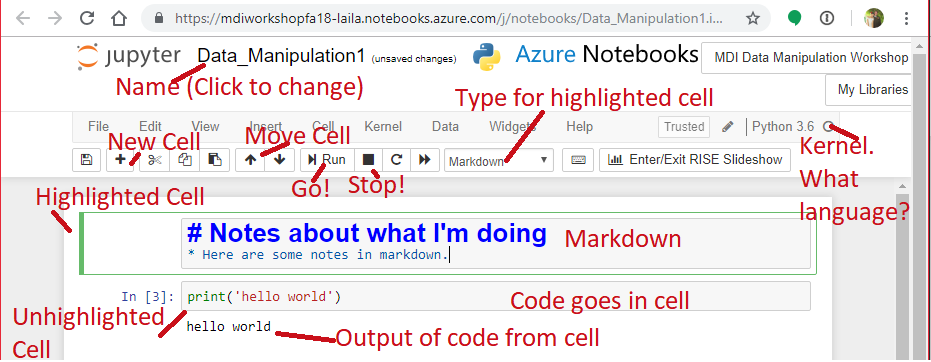
Network Analysis in Python¶
Laila A. Wahedi, PhD¶
Massive Data Institute Postdoctoral Fellow
McCourt School of Public Policy
Follow along:¶
- Slides: http://Wahedi.us, Tutorial
- Interactive Notebook: https://notebooks.azure.com/Laila/projects/mdi-network-analysis-workshop
Follow Along¶
- Go to https://notebooks.azure.com/Laila/libraries/MDI-workshopFA18
- Clone the directory
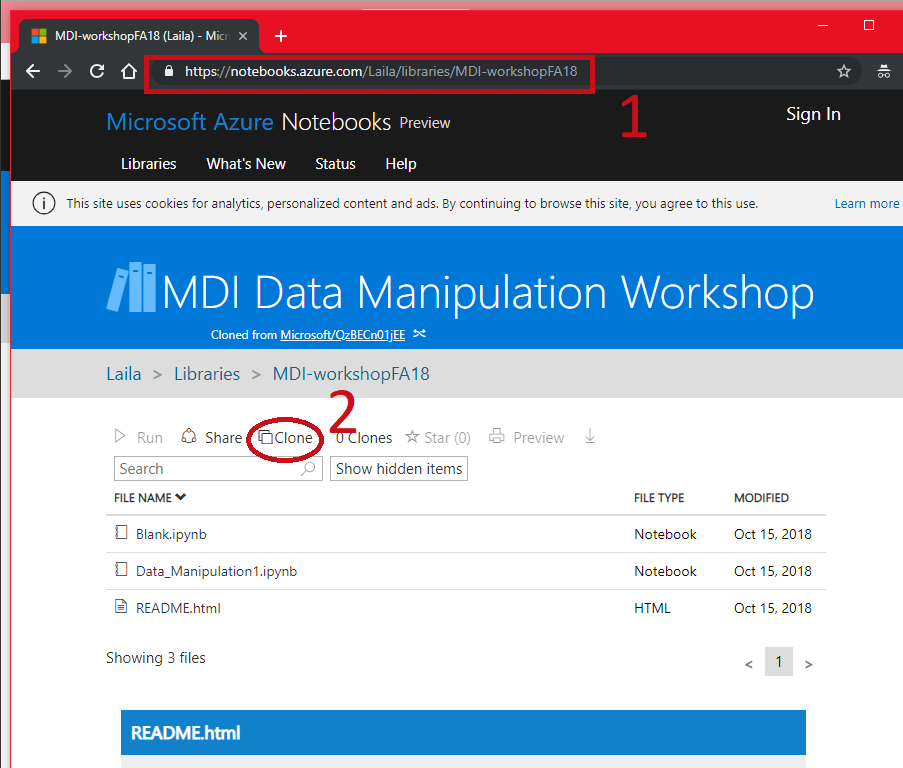
Follow Along¶
- Sign in with any Microsoft Account (Hotmail, Outlook, Azure, etc.)
- Create a folder to put it in, mark as private or public
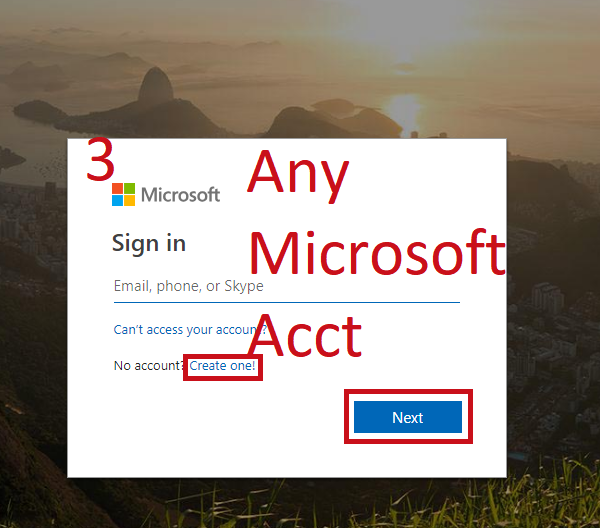
Follow Along¶
- Open a notebook
- Open this notebook to have the code to play with
- Open a blank notebook to follow along and try on your own.
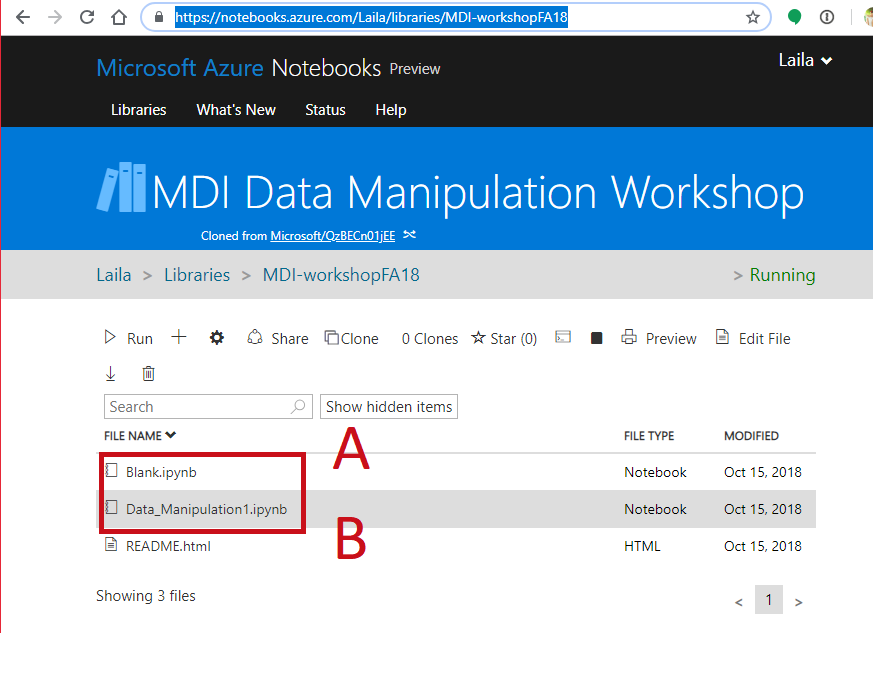
Your Environment¶
- Jupyter Notebook Hosted in Azure
- Want to install it at home?
- Install the Anaconda distribution of Python https://www.anaconda.com/download/
- Install Jupyter Notebooks http://jupyter.org/install
In [1]:
foo = 'some variable content'
In [2]:
print(foo)
some variable content
Your Environment: Saving¶
- If your kernel dies, data are gone.
- Not R or Stata, you can't save your whole environment
- Data in memory more than spreadsheets
- Think carefully about what you want to save and how.
Easy Saving: Pickle¶
- dump to save the data to hard drive (out of memory)
Contents of the command:
- variable to save,
- File to dump the variable into:
- open(
"name of file in quotes",
"wb") "Write Binary"
- open(
Note: double and single quotes both work
In [ ]:
mydata = [1,2,3,4,5,6,7,8,9,10]
pickle.dump(mydata, open('mydata.p','wb'))
mydata = pickle.load(open("mydata.p","rb"))
Get your environment ready¶
- We'll cover the basics later, for now start installing and loading packages by running the following code:
In [2]:
import networkx as nx
import pandas as pd
import numpy as np
import pickle
import matplotlib.pyplot as plt
%matplotlib inline
What is a network?¶
- Nodes/ Vertices
- Links/ edges/ ties/ arcs
- Weights
- Also called a graph
Bipartite: Networks with two types of node¶
- People and the stores they shop in
- Movies and actors
- Words and authors
- What are some other examples?
Weighted: Networks with ties of different strength¶
- Twitter users linked by number of retweets
- People linked by distance between homes
- Cities linked by dollars of trade
- Cities linked by number of travelers
Directed Networks:¶
Edges are not always symmetrical¶
- Twitter user @Ahmad may retweet @Bethany more often than @Bethany retweets Ahmad
- Mexico buys from the US more than the US buys from Mexico
- User mentions on Twitter
- Outgoing phone calls between people
- Friendship rankings: Bobathy may list Amira as a friend on a survey without Amira listing Bobathy
Weighted and directed networks are related. Which are weighted and which are unweighted?¶
When are weighted networks not directed?¶
Representing a Network: Edge List¶
- Dyads
- Each row contains a pair of nodes indicating a tie
- A Third Column Cindicates weight
- Order may indicate direction of edge
In [30]:
edges = [('Fred', 'Maria'),
('Fred', 'Samir'),
('Fred', 'Jose',),
('Maria', 'Sonya',),
('Samir','Jose'),
('Samir','Sonya'),]
Make this a weighted, undirected network¶
In [25]:
edges_weighted = [('Fred', 'Maria', 3),
('Fred', 'Samir', 6),
('Fred', 'Jose', 2),
('Maria', 'Sonya', 1),
('Samir','Jose',3),
('Samir','Sonya',5)]
What would you need to do to make this directed?¶
In [63]:
edges_directed = [('Fred', 'Maria', 3),
('Fred', 'Samir', 6),
('Fred', 'Jose', 2),
('Maria', 'Sonya', 1),
('Samir','Jose',3),
('Samir','Sonya',5),
('Maria', 'Fred', 2),
('Samir', 'Fred', 4),
('Jose', 'Fred', 6),
('Sonya', 'Maria', 3),
('Jose','Samir',3),]
Representing a network: Adjacency Matrix¶
- nxn matrix of nodes, where position i,j indicates relationship between node i and node j
- Index position corresponds with nodes. Keep the order straight
- Can be symmetrical or directed, use weights or indicators with 1
- Less space efficient for sparse networks, but convenient for linear algebra operations
- Use Numpy package, imported as np to make matrices
- Index as (row, column)
- Why: Do matrix operations on whole network
Representing a network: Adjacency Matrix¶
In [48]:
adj = np.zeros((5,5))
edge_index = [(0,1),(0,2),(0,3),
(1,0),(1,4),
(2,0),(2,3),(2,4),
(3,0),(3,2),
(4,1),(4,2)]
for p in edge_index:
adj[p] = 1
adj
Out[48]:
array([[ 0., 1., 1., 1., 0.],
[ 1., 0., 0., 0., 1.],
[ 1., 0., 0., 1., 1.],
[ 1., 0., 1., 0., 0.],
[ 0., 1., 1., 0., 0.]])
Representing a network: Adjacency Matrix¶
- To keep your labels, use the Pandas package, imported as pd
In [16]:
nodes = ['Fred','Maria','Samir','Jose','Sonya','Freya','Hasan']
adj_labeled = pd.DataFrame(adj,columns=nodes,index=nodes)
adj_labeled
Out[16]:
| Fred | Maria | Samir | Jose | Sonya | |
|---|---|---|---|---|---|
| Fred | 0.0 | 1.0 | 1.0 | 1.0 | 0.0 |
| Maria | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| Samir | 1.0 | 0.0 | 0.0 | 1.0 | 1.0 |
| Jose | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| Sonya | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 |
Representing A network in Python: Networkx Object¶
- Using the networkx package, imported as nx
- Package designed to hold network data, visualize it, and to perform basic exploratory analysis
Instantiating Our Network¶
- Declare a graph object
- Graph is another term for network
- Add your nodes or vertices
- Add your edges from an edgelist
In [149]:
G = nx.Graph()
G.add_nodes_from(nodes)
G.add_edges_from(edges)
G
Out[149]:
<networkx.classes.graph.Graph at 0x7f6a14a1f978>
In [33]:
print(G.nodes)
['Fred', 'Maria', 'Samir', 'Jose', 'Sonya']
{'Maria': {}, 'Samir': {}, 'Jose': {}}
In [39]:
G.edges()
Out[39]:
EdgeView([('Fred', 'Maria'), ('Fred', 'Samir'), ('Fred', 'Jose'), ('Maria', 'Sonya'), ('Samir', 'Jose'), ('Samir', 'Sonya')])
In [40]:
print(G['Fred'])
{'Maria': {}, 'Samir': {}, 'Jose': {}}
Add Some Friends¶
In [49]:
G.add_nodes_from(['Freya','Hasan'])
G.add_edges_from([('Sonya','Freya'),('Sonya','Hasan')])
In [51]:
nx.draw_networkx(G, with_labels = True)
Make a Weighted Network:¶
- Add weighted edges instead of unweighted edges
- Stores weight attribute in the edges
- Can also store node attributes
In [59]:
G_weighted = nx.Graph()
G_weighted.add_nodes_from(nodes)
G_weighted.add_weighted_edges_from(edges_weighted)
nx.set_node_attributes(G_weighted,
{'Fred':16,
'Maria:':15,
'Samir':15,
'Jose':15,
'Sonya':14},
'age')
Make a Directed Network:¶
- Use a DiGraph object
- Can also use weighted edges
- Stores weight attribute in the edges
In [79]:
G_dir = nx.DiGraph()
G_dir.add_nodes_from(nodes)
G_dir.add_weighted_edges_from(edges_directed)
nx.set_node_attributes(G_dir,
{'Fred':16, 'Maria:':15,
'Samir':15,'Jose':15,
'Sonya':14}, 'age')
View Your Data:¶
- Friends are no longer symmetrical
In [66]:
print(G_dir['Samir'])
print(G_dir['Jose'])
{'Jose': {'weight': 3}, 'Sonya': {'weight': 5}, 'Fred': {'weight': 4}}
{'Fred': {'weight': 6}, 'Samir': {'weight': 3}}
View Your Data:¶
- View node attributes
- View weights
In [81]:
G_dir.nodes['Samir']['age']
Out[81]:
15
In [84]:
G_dir['Samir']['Fred']['weight']
Out[84]:
4
Make a Bipartite Network:¶
- Two node sets
- Edges between node sets
- No edges within node sets
In [106]:
G_bi = nx.Graph()
G_bi.add_nodes_from(['Georgetown',
'George Mason',
'George Washington'],
bipartite = 0)
G_bi.add_nodes_from(['Fred','Jose',
'Ayesha','Sara',
'Bethany','Bobathy'],
bipartite = 1
)
Make a Bipartite Network:¶
- Two node sets
- Edges between node sets
- No edges within node sets
In [107]:
G_bi.add_edges_from([('Georgetown','Fred'),
('Georgetown','Jose'),
('Georgetown','Ayesha'),
('George Washington','Fred'),
('George Washington','Jose'),
('George Washington','Sara'),
('George Mason','Bethany'),
('George Mason','Bobathy')
])
Project to unipartite¶
- Ties between universities that admitted the same students
- Bipartite set treated as attribute label
In [112]:
schools = []
for node, data in G_bi.nodes(data=True):
if data['bipartite']==0:
schools.append(node)
G_schools = nx.bipartite.projected_graph(G_bi, schools)
nx.draw_networkx(G_schools, with_labels=True)
Make G_bi a weighted graph¶
In [113]:
G_bi.add_weighted_edges_from([('Georgetown','Fred',10000),
('Georgetown','Jose',0),
('Georgetown','Ayesha',20000),
('George Washington','Fred',7000),
('George Washington','Jose',10000),
('George Washington','Sara',0),
('George Mason','Bethany',30000),
('George Mason','Bobathy',0)
])
Back to the Friendship Network¶
- Who is most popular?
- Who is most powerful?
- Why?
In [114]:
nx.draw_networkx(G)
Degree Centrality¶
- Number of ties, or normalized number of ties
- Sum of rows
- In-degree: number of edges to a node
- Out-degree: number of edges from a node
- When?
In [115]:
deg = nx.degree_centrality(G)
print(deg)
{'Fred': 0.5, 'Maria': 0.3333333333333333, 'Samir': 0.5, 'Jose': 0.3333333333333333, 'Sonya': 0.6666666666666666, 'Freya': 0.16666666666666666, 'Hasan': 0.16666666666666666}
Eigenvector Centrality¶
- Connectedness to other well-connected nodes
Theoretical Implication: A lot of work to maintain ties to everyone, sometimes just as good to know someone who knows everyone.
- Finding a job
- Rumors
- Supply
Requires connected network
- Cannot compare across networks
When might eigenvector centrality be less useful?¶
Calculating Eigenvector Centrality¶
- Take eigenvector for maximum eigenvalue
- nx.eigenvector_centrality uses a different method that usually converges to the same result, but sometimes errors.
In [116]:
eig_c = nx.eigenvector_centrality_numpy(G)
toy_adj = nx.adjacency_matrix(G)
print(eig_c)
val,vec = np.linalg.eig(toy_adj.toarray())
print(val)
vec[:,0]
{'Fred': 0.46672895953759114, 'Maria': 0.35495662631912422, 'Samir': 0.49598948281898347, 'Jose': 0.36847650119192471, 'Sonya': 0.4606661098595255, 'Freya': 0.17631804784296684, 'Hasan': 0.17631804784296681}
[ 2.6126997 1.34352222 -2.29002215 0.28331905 -1.24305532 -0.70646349
0. ]
Out[116]:
array([-0.46672896, -0.35495663, -0.49598948, -0.3684765 , -0.46066611,
-0.17631805, -0.17631805])
Betweenness Centrality¶
- Proportional to the number of shortest paths that pass through a given node
- How important is that node in connecting other nodes
In [117]:
betw = nx.betweenness_centrality(G)
print(betw)
{'Fred': 0.1, 'Maria': 0.1, 'Samir': 0.3, 'Jose': 0.0, 'Sonya': 0.6333333333333333, 'Freya': 0.0, 'Hasan': 0.0}
Centrality Measures Are Different¶
- Select based on theory you want to capture
- Correlation between measures differs across networks
- Take a minute to play around with the network and see how the relationships change
In [119]:
cent_scores = pd.DataFrame({'deg':deg,'eig_c':eig_c,'betw':betw})
print(cent_scores.corr())
cent_scores
deg eig_c betw deg 1.000000 0.914429 0.860781 eig_c 0.914429 1.000000 0.628927 betw 0.860781 0.628927 1.000000
Out[119]:
| deg | eig_c | betw | |
|---|---|---|---|
| Fred | 0.500000 | 0.466729 | 0.100000 |
| Freya | 0.166667 | 0.176318 | 0.000000 |
| Hasan | 0.166667 | 0.176318 | 0.000000 |
| Jose | 0.333333 | 0.368477 | 0.000000 |
| Maria | 0.333333 | 0.354957 | 0.100000 |
| Samir | 0.500000 | 0.495989 | 0.300000 |
| Sonya | 0.666667 | 0.460666 | 0.633333 |
Difference in Measures¶
- Sonya has the most friends
- Sonya's friends are not as well connected, lowering her eigenvector centrality
- Fred and Samir have better connected friends
- Hasan and Freya have no connection to the others except through Sonya, giving her high betweenness
In [120]:
nx.draw_networkx(G)
Florentine Marriage Networks¶
- Families in this graph are connected when there are marriage ties between them
- Calculate the centrality scores
- Who is the most powerful?
In [137]:
florentine = nx.generators.social.florentine_families_graph()
nx.draw_networkx(florentine)
Florentine Centrality¶
In [136]:
deg = nx.degree_centrality(florentine)
betw = nx.betweenness_centrality(florentine)
eigc = nx.eigenvector_centrality(florentine)
cent_scores = pd.DataFrame({'deg':deg,'eig_c':eigc,'betw':betw})
cent_scores.sort_values(['deg','eig_c','betw'])
Out[136]:
| deg | eig_c | betw | |
|---|---|---|---|
| Pazzi | 0.071429 | 0.044815 | 0.000000 |
| Ginori | 0.071429 | 0.074925 | 0.000000 |
| Lamberteschi | 0.071429 | 0.088793 | 0.000000 |
| Acciaiuoli | 0.071429 | 0.132157 | 0.000000 |
| Salviati | 0.142857 | 0.145921 | 0.142857 |
| Barbadori | 0.142857 | 0.211706 | 0.093407 |
| Albizzi | 0.214286 | 0.243961 | 0.212454 |
| Castellani | 0.214286 | 0.259020 | 0.054945 |
| Peruzzi | 0.214286 | 0.275722 | 0.021978 |
| Bischeri | 0.214286 | 0.282794 | 0.104396 |
| Tornabuoni | 0.214286 | 0.325847 | 0.091575 |
| Ridolfi | 0.214286 | 0.341554 | 0.113553 |
| Guadagni | 0.285714 | 0.289117 | 0.254579 |
| Strozzi | 0.285714 | 0.355973 | 0.102564 |
| Medici | 0.428571 | 0.430315 | 0.521978 |
Florentine Centrality¶
- Which measure best captures Medici power? Why?
- What's up with Guadagni's betweenness vs Stozzi?
- Why does Strozzi have high eigenvector centrality?
Karate Club Graph¶
- Compare 0 and 32/33
- Shared influence
- Compare 5/6 with 27/28
- Neighborhood density
- Why is eigenvector better correlated with degree here than in our friend graph?
- Triangles!
In [132]:
karate = nx.generators.social.karate_club_graph()
nx.draw_networkx(karate)
Karate Club Graph¶
- Compare 0 and 32/33
- Shared influence
- Compare 5/6 with 27/28
- Neighborhood density
- Why is eigenvector better correlated with degree here than in our friend graph?
- Triangles!
In [139]:
deg = nx.degree_centrality(karate)
betw = nx.betweenness_centrality(karate)
eigc = nx.eigenvector_centrality(karate)
cent_scores = pd.DataFrame({'deg':deg,'eig_c':eigc,'betw':betw})
cent_scores.sort_values(['deg','eig_c','betw'])
Out[139]:
| deg | eig_c | betw | |
|---|---|---|---|
| 11 | 0.030303 | 0.052854 | 0.000000 |
| 16 | 0.060606 | 0.023635 | 0.000000 |
| 26 | 0.060606 | 0.075582 | 0.000000 |
| 12 | 0.060606 | 0.084252 | 0.000000 |
| 17 | 0.060606 | 0.092397 | 0.000000 |
| 21 | 0.060606 | 0.092397 | 0.000000 |
| 14 | 0.060606 | 0.101406 | 0.000000 |
| 15 | 0.060606 | 0.101406 | 0.000000 |
| 18 | 0.060606 | 0.101406 | 0.000000 |
| 20 | 0.060606 | 0.101406 | 0.000000 |
| 22 | 0.060606 | 0.101406 | 0.000000 |
| 9 | 0.060606 | 0.102675 | 0.000848 |
| 24 | 0.090909 | 0.057054 | 0.002210 |
| 25 | 0.090909 | 0.059208 | 0.003840 |
| 10 | 0.090909 | 0.075966 | 0.000631 |
| 4 | 0.090909 | 0.075966 | 0.000631 |
| 28 | 0.090909 | 0.131079 | 0.001795 |
| 19 | 0.090909 | 0.147911 | 0.032475 |
| 6 | 0.121212 | 0.079481 | 0.029987 |
| 5 | 0.121212 | 0.079481 | 0.029987 |
| 27 | 0.121212 | 0.133479 | 0.022333 |
| 29 | 0.121212 | 0.134965 | 0.002922 |
| 7 | 0.121212 | 0.170955 | 0.000000 |
| 30 | 0.121212 | 0.174760 | 0.014412 |
| 23 | 0.151515 | 0.150123 | 0.017614 |
| 13 | 0.151515 | 0.226470 | 0.045863 |
| 8 | 0.151515 | 0.227405 | 0.055927 |
| 31 | 0.181818 | 0.191036 | 0.138276 |
| 3 | 0.181818 | 0.211174 | 0.011909 |
| 1 | 0.272727 | 0.265954 | 0.053937 |
| 2 | 0.303030 | 0.317189 | 0.143657 |
| 32 | 0.363636 | 0.308651 | 0.145247 |
| 0 | 0.484848 | 0.355483 | 0.437635 |
| 33 | 0.515152 | 0.373371 | 0.304075 |
Speaking of triangles: Transitivity¶
- Extent to which friends have friends in common
- Probability two nodes are tied given that they have a partner in common
- Make a more transitive network:
In [146]:
G_trans = G.copy()
G_trans.add_edges_from([('Samir','Maria')])
nx.draw_networkx(G_trans)
Transitivity¶
- Extent to which friends have friends in common
- Probability two nodes are tied given that they have a partner in common ### Look at transitivity and triangles in the two networks
In [150]:
print("Transitivity:")
print(nx.transitivity(G))
print(nx.transitivity(G_trans))
print("Triangles:")
print(nx.triangles(G))
print(nx.triangles(G_trans))
Transitivity:
0.3333333333333333
0.47368421052631576
Triangles:
{'Fred': 1, 'Maria': 0, 'Samir': 1, 'Jose': 1, 'Sonya': 0}
{'Fred': 2, 'Maria': 2, 'Samir': 3, 'Jose': 1, 'Sonya': 1, 'Freya': 0, 'Hasan': 0}
Clustering Coefficient¶
- Individual Nodes:
- Proportion of possible triangles through a given node
- Whole Network
- Average clustering across whole network
In [151]:
print("Clustering coefficient")
print(nx.clustering(G))
print(nx.clustering(G_trans))
print("Average Clustering")
print(nx.average_clustering(G))
print(nx.average_clustering(G_trans))
Clustering coefficient
{'Fred': 0.3333333333333333, 'Maria': 0, 'Samir': 0.3333333333333333, 'Jose': 1.0, 'Sonya': 0}
{'Fred': 0.6666666666666666, 'Maria': 0.6666666666666666, 'Samir': 0.5, 'Jose': 1.0, 'Sonya': 0.16666666666666666, 'Freya': 0, 'Hasan': 0}
Average Clustering
0.3333333333333333
0.4285714285714285
Which is more clustered? Florentine or Karate?¶
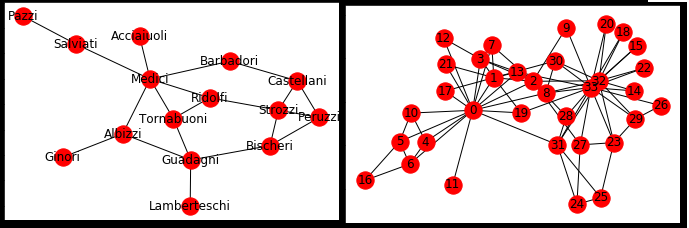
Florentine has few triangles¶
In [158]:
nx.draw_networkx(florentine)
nx.average_clustering(florentine)
Out[158]:
0.16
Karate Club has a lot of triangles¶
- Why might they be different?
In [159]:
nx.draw_networkx(karate)
nx.average_clustering(karate)
Out[159]:
0.5706384782076823
Different Structures Are Produced by and Produce Different Behaviors¶
- Triadic closure -> transitivity on friendship network
- Less redundancy in strategic Medicci marriage contracts. Triangles inefficient
- Clustering captures tendency toward closure globally. What might it miss?
What might we miss?¶
In [174]:
squares = nx.Graph()
se = [(0,1),(1,2),(2,3),(3,0),(0,5),(4,5),(3,4),
(5,6),(6,7),(7,0),(2,8),(8,9)]
se2 = [(i[0]+9,i[1]+9) for i in se[:-2]]
se.extend(se2)
squares.add_nodes_from(range(17))
squares.add_edges_from(se)
nx.draw_networkx(squares)
nx.average_clustering(squares)
Out[174]:
0.0
What Can We Do?¶
- Count n-cycles.
- Count all cycles, keep those below threshold
In [175]:
nx.cycle_basis(squares)
Out[175]:
[[5, 6, 7, 0], [3, 4, 5, 0], [1, 2, 3, 0], [14, 15, 16, 9], [12, 13, 14, 9], [10, 11, 12, 9]]
What Can We Do?¶
- Square clustering ### Intuitive names like clustering are nice, but always know what you're measuring and check if it's appropriate for your network
In [190]:
clustering_coefs = nx.square_clustering(squares).values()
np.mean(list(clustering_coefs))
Out[190]:
0.6147058823529411
Community Detection¶
- Divide the network into subgroups using different algorithms
- Examples
- Percolation: find communities with fully connected cores
- Minimum cuts (nodes): Find the minimum number of nodes that, if removed, break the network into multiple components. Progressively remove them.
- Girvan Newman Algorithm: Remove ties with highest betweenness, continue until network broken into desired number of communities
In [145]:
coms = nx.algorithms.community.centrality.girvan_newman(G)
i = 2
for com in itertools.islice(coms,4):
print(i, ' communities')
i+=1
print(tuple(c for c in com))
2 communities
({'Jose', 'Maria', 'Samir', 'Fred'}, {'Freya', 'Hasan', 'Sonya'})
3 communities
({'Jose', 'Maria', 'Samir', 'Fred'}, {'Hasan', 'Sonya'}, {'Freya'})
4 communities
({'Jose', 'Samir', 'Fred'}, {'Maria'}, {'Hasan', 'Sonya'}, {'Freya'})
5 communities
({'Fred'}, {'Maria'}, {'Samir', 'Jose'}, {'Hasan', 'Sonya'}, {'Freya'})
Why Detect Communities¶
- Learn something about how an unknown network is organized
- Generate hypotheses.
- Why did these communities emerge?
- How do these communities affect the behavior of members?
- How do they relate to attributes of the members?
- How do they evolve over time, how do different networks compare?
What are some examples?¶
Assessing Community Detection:¶
- Density: Number of ties / maximum number
- Maximum number of ties: Every node in network has a tie
- Modularity: Fraction of edges within a group / expected edges in random graph
- Is the density within each community greater than a random network generated with the same density of the overall network
In [198]:
nx.density(G)
Out[198]:
float
Preview: Random Graphs¶
- Different methods to capture different properties
- Compare random graph with desired properties to real graph
- Today: Erdos-Renyi Graph
- Takes all possible edges
- Each edge has a probability p of being realized
- Produces graph with desired average density
- Does not capture other properties common in real world graphs #### More next week!
In [209]:
G_rand = nx.gnp_random_graph(len(karate.nodes),
nx.density(karate))
nx.draw_networkx(G_rand)
Modularity and Random Graphs¶
- Compare number of ties within community to expected number if the graph were an Erdos Renyi Graph
In [220]:
nx.average_clustering(karate)
Out[220]:
0.5706384782076823
In [221]:
nx.average_clustering(G_rand)
Out[221]:
0.1254435107376284
Compare the clustering visually:¶
In [231]:
#View clusters
plt.hist(nx.clustering(karate).values(), alpha = .5)
plt.hist(nx.clustering(G_rand).values(), alpha = .5)
Out[231]:
(array([ 11., 1., 2., 4., 3., 3., 5., 0., 0., 5.]),
array([ 0. , 0.03333333, 0.06666667, 0.1 , 0.13333333,
0.16666667, 0.2 , 0.23333333, 0.26666667, 0.3 ,
0.33333333]),
<a list of 10 Patch objects>)
Compare the clustering in florentine to a random network¶
- How do they differ?
In [227]:
G_rand_f = nx.gnp_random_graph(len(florentine.nodes),
nx.density(florentine))
nx.draw_networkx(G_rand_f)
Compare the clustering in florentine to a random network¶
- How do they differ?
In [230]:
print('Florentine: ',nx.average_clustering(florentine))
print('Random: ', nx.average_clustering(G_rand_f))
plt.hist(nx.clustering(florentine).values(),alpha=.5)
plt.hist(nx.clustering(G_rand_f).values(), alpha = .5)
florentine: 0.16 random: 0.28444444444444444
Out[230]:
(array([ 5., 1., 2., 4., 0., 1., 1., 0., 0., 1.]), array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ]), <a list of 10 Patch objects>)
Modularity Based Performance Measurement¶
- Modularity: Fraction of edges within group - expected number of edges
- Networkx performance metric:
- (Number of edges within groups - Number of edges between groups)/(Total Edges)
In [318]:
coms = nx.algorithms.community.centrality.girvan_newman(squares)
for com in itertools.islice(coms,1):
partition = tuple(list(c) for c in com)
nx.algorithms.community.quality.performance(squares,partition)
Out[318]:
0.6764705882352942
Compare the insularity of the communities in the florentine and karate networks¶
- Why is it that so?
In [310]:
coms = nx.algorithms.community.centrality.girvan_newman(karate)
for com in itertools.islice(coms,1):
k_partition = tuple(list(c) for c in com)
nx.algorithms.community.quality.performance(karate,k_partition)
Out[310]:
0.6114081996434938
In [347]:
coms = nx.algorithms.community.centrality.girvan_newman(florentine)
for com in itertools.islice(coms,1):
fl_partition = tuple(list(c) for c in com)
nx.algorithms.community.quality.performance(florentine,fl_partition)
Out[347]:
0.41904761904761906
Visualizing the networks¶
- Matplotlib package, imported as plt
- %matplotlib inline magic to make it plot in the notebook
In [357]:
order = adj_labeled.sum().sort_values().index
adj_labeled = adj_labeled.loc[order,order]
plt.figure(figsize = (8,6))
plt.pcolor(adj_labeled,cmap=plt.cm.RdBu)
plt.yticks(np.arange(0.5, 5, 1), adj_labeled.index, fontsize = 20)
plt.xticks(np.arange(0.5, 5, 1), adj_labeled.columns, rotation =45, ha='right', fontsize=20 )
plt.title('Adjacency\n',fontsize=20)
cbar =plt.colorbar()
Graph Plotting Algorithms¶
- Can learn something by placing the nodes in an intelligent way
- Force Algorithm: Put nodes that are connected closer together
In [358]:
plt.figure(figsize=(15,15))
pos = nx.spring_layout(florentine)
deg = nx.degree(florentine)
deg = [deg[k]*400 for k in florentine.nodes]
nx.draw_networkx(florentine,pos=pos, with_labels=True,
node_size=deg,font_size=30)
Add Color¶
In [359]:
plt.figure(figsize=(15,15))
colors = []
for n in florentine.nodes:
if n in fl_partition[0]:
colors.append('blue')
else:
colors.append('red')
nx.draw_networkx(florentine,pos=pos, with_labels=True,
node_size=deg,font_size=30, node_color = colors)
Draw the Florentine Network with Three Partitions¶
In [360]:
coms = nx.algorithms.community.centrality.girvan_newman(florentine)
for com in itertools.islice(coms,2):
fl_partition = tuple(list(c) for c in com)
nx.algorithms.community.quality.performance(florentine,fl_partition)
colors = []
for n in florentine.nodes:
if n in fl_partition[0]:
colors.append('blue')
elif n in fl_partition[1]:
colors.append('red')
else:
colors.append('green')
plt.figure(figsize=(15,15))
nx.draw_networkx(florentine,pos=pos, with_labels=True,
node_size=deg,font_size=30, node_color = colors)
Next Time: Making Inferences¶
- Network Questions
- Network Properties
- Degree distributions
- Centralization
- Random Networks
- Regressions with Network Variables